Puzzles (1)

Besides the chess compositions (the chess problems), there are many chess puzzles, that use chessboards and chessmen, but their subject is basically mathematic.
The chessmen have various abilities, thus we can "play" with various positionings or moves of the pieces.

Let us see some puzzles, easy enough.
I expect solutions like [Puzzle_x, solution / solutions].
On the internet the solutions surely exist. You do not need to search there.
What I ask from you is to face the challenge by yourself and discover one solution. If you like, find how many distinct (not by turning the chessboard, not mirror positions) solutions exist for this puzzle.

P001 : How many, at most, white rooks can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P002 : How many, at most, white queens can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P003 : How many, at most, white knights can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P004 : On a chessboard we see many squares, of various sizes (1x1, 2x2, 3x3, ..., 8x8), with sides parralel with the sides of the chessboard. How many are they?

---

Answers

My thanks to the reader HeinzK (see his blog) who sent a comment.

Puzzle_001 : How many, at most, white rooks can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P001 P001a

We can place, easily, 8 rooks. The obvious solution is to place them on one main diagonal (See P001). We could also place them differently, having each rook guard a line and a file (See P001a). If we accept that the firs rook can be placed on one square of the first file, then the second rook can occupy one of seven squares in the second file, etc, until the eighth rook can be placed on one free square of the eighth file. Totally there are 8*7*6*5*4*3*2*1 positions, (in mathematics this product is named [8 factorial] and is denoted by [8!]), so we have 8!=40320 positions. The Greek friend Carlo DeGrandi informs us that the problem was described first by the English mathematician Ernest Dudeney (1857-1930), who has also invented the crossing of words into crosswords.

Puzzle_002 : How many, at most, white queens can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P002

We can place, with a little difficulty, 8 queens. The king of the puzzles, (there is a book "The Puzzle King" with his chess puzzles, by Sid Pickard), the American Sam Loyd has published in the American Chess Journal in February 1877 the position you see in P002, (stretching the fact that whichever the solution, with rotation or mirroring we will have a queen on d1). This is an old problem, (a comment by Kevin notes that it was first proposed by Max Bezzel, in Die Schachzeitung, 1848), it was published in 1848 in the German chess magazine "Illustrierte Scachzeitung" (=Illustrated Chess newspaper) as follow-up on a question by the philologist professor Dr. A. Nauck, who also proposed to Karl Friedrich Gauss (1777-1855) this problem. Nauck has published in 1850 a solution (mirror image of the solution by Loyd) while the mathematician Gauss has found 12 basic solutions. (See here). This type of problem is very popular to the students of informatics.

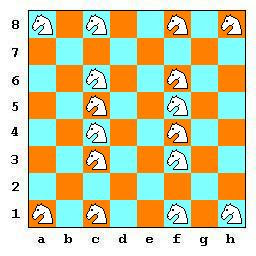
Puzzle_003 : How many, at most, white knights can we place on a chessboard 8x8, to guard all squares except the occupied ones?

P003a P003b P003c

The answer is very easy : 32. We place 32 knights on the white squares of the chessboard and they all "threat" the black squares. Alternatively, we could place them all on black squares. Thus, we have two solutions. With a modified formulation Puzzle_3a : "How many, at least, white knights can we place on a chessboard 8x8, to guard all squares except the occupied ones?", we see an easy answer (figure P003a) which uses 24 knights, an one more economic with 16 knights (figure P003b). Modifying again the formulation Puzzle_3b : "How many, at least, white knights can we place on a chessboard 8x8, to guard all non-occupied squares?", (meaning that some occupied squares could be guarded), we find that the best solution (figure P003c) uses only 12 knights!

Puzzle_004 : On a chessboard we see many squares, of various sizes (1x1, 2x2, 3x3, ..., 8x8), with sides parralel with the sides of the chessboard. How many are they?
P004	On figure P004 we see numbers inside the squares of the chessboard. This number is the multitude of various-sized squares formed with this square as the upper-left-corner. Adding these multitudes (as shown in the margin) we have total = 1x8 + (2x7+1x7) + (3x6+2x6) + (4x5+3x5) + (5x4+4x4) + (6x3+5x3) + (7x2+6x2) + (8x1+7x1) = 8 + 21 + 30 + 35 + 36 + 33 + 26 + 15 = 204 squares.